From wikipedia:
In mathematics, the dot product, also known as the scalar product, is a binary operation which takes two vectors and returns a scalar quantity. It is the standard inner product of the Euclidean space.
The dot product of two vectors a = [a1, a2, … , an] and b = [b1, b2, … , bn] is by definition
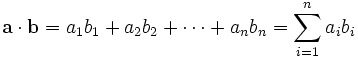
where Σ denotes summation notation. For example, the dot product of two three-dimensional vectors [1, 3, −2] and [4, −2, −1] is
- [1, 3, −2]·[4, −2, −1] = 1×4 + 3×(−2) + (−2)×(−1) = 0.
Using matrix multiplication and treating the row vectors as 1×n matrices, the dot product can also be written as
where bT denotes the transpose of the matrix b. Using the example from above, this would result in a 1×3 matrix (i.e. vector) multiplied by a 3×1 vector (which, by virtue of the matrix multiplication, results in a 1×1 matrix):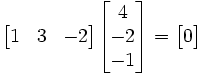
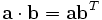
No comments:
Post a Comment