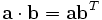Array = homogenous collection
q: what types for subscripts, do we rangecheck, are ranges bound, array alloc when, how many subscripts (1,2), initialization, are slices allowed?
FORTRAN:
SUM = SUM + B(I)
same () as functions so needs keep track. why? no other chars avail. Ada as well - because both are mappings of parameters to values. Pascal, C++, Java = []
obvious point: element type vs. subscript type. most often subrange of int. Pascal, Ada: Bool, char, enum.
subrange checking: Pascal, Ada, Java. Not C++, FORTRAN - out of bound errors. speed vs. reliability.
Binding of subscript type statically bound (usually) but value range can s/t vary dynamically.
lower bound: 0, 1, set by user.
4 cat, based on binding to subscript range and binding to storage.
static array - both ranges and binding to storage at compile time. no dynamic alloc dealloc. FORTRAN 77.
fixed stack-dynamic - subscripts bound statically, storage bound off the stack - C, Pascal.
stack-dynamic - same as above but subscript bound dynamically as well. but then remain fixed for lifetime of var. Ada:
GET (LIST_LEN)
declare
LIST : array (1..LIST_LEN) of INTEGER
begin
...
end
heap-dynamic - same, but can change many times during lifetime. FORTRAN 90:
INTEGER, ALLOCATABLE, ARRAY (:, :) :: MAT
ALLOCATE (MAT(10, NUMBER_OF_COLUMNS)
DEALLOCATE(MAT)
same idea in C, C++ using pointers.
Number of Subscripts
saw in fortran assignment that could use mult indices. original fortran restricted to 3. The ZERO-ONE-INFINITE principle. Let programmer bear the cost if he wants. FORTRAN IV it became 7. Modern - unlimited.
Array init: FORTRAN has it in the form of a DATA statement:
DATA MYVAR / 8, 9, 10/
in C, init of arrays, of strings, of arrays of strings. In Java.
Ada:
LIST : array (1..5) of INTEGER := (1, 4, 6, 8, 10)
LIST : array (1..5) of INTEGER := (1 => 3, 4 => 9, others =>0)
array ops
to be continued...
Tuesday, February 28, 2006
Data Types 2
Posted by
joshwaxman
at
12:57 PM
0
comments
![]()
Thursday, February 23, 2006
Class Notes - Data Types - 1
Lifetime
Not same as scope. Example – subprogram in C where exists but hidden. Static in C.
Symbolic constants
Why? Readability. Reliability. Ease of changing the program. We saw in the program where can be useful. Two types – lvalues and rvalues. Const vs. #define.
Pascal - simple, Modula-2: complex expressions. manifest constants –simple due to static binding of values.
C++, Java, Ada: constants based on variables – bound at runtime
Initializing Variables
We know C++. int x = 6; FORTRAN has DATA statement
REAL PI
INTEGER SUM
DATA SUM /0/, PI /3.14/
Some langs do not have init statements. Just do assignment. Pascal.
When is this initialization done? Static vs. auto in C.
ALGOL 60
First, ALGOL 58, designed by international committee. 3 goals: close to standard mathematical notation; use to describe computing processes in publications; able to translate to machine code. JOVIAL, MAD, NELIAC. In general, taken to be guidelines for developing langs. IBM interested in promoting FORTRAN.
ALGOL 60, Peter Naur described using BNF, which while elegant, was not well understood back then.
Contributions: many langs based on this. Example: pascal, ALGOL 68, Ada, C++, PL/I, Java. Was only accepted way of describing algorithms. Influenced machine architecture to implement the concepts. Advances: block structure; pass by value and pass by name. recursive procs. Stack dynamic arrays. (now they have them in C, I think). But lacked standard IO = difficulty porting. People already using FORTRAN.
I posted before an initial ALGOL reading – 95 – 121. A summary of material covered there – Algol 58, use of BNF (with further discussion in next chapter), Algol 60. Blocks. Though ALGOL has static scoping, a discussion of dynamic scoping. Pg 118. generalized arrays by allowing lower bounds, dynamic arrays. Pg 119 – strong typing. Look thru the code.
Now 121-140. A lot of what we discussed. Pass by name, value. Recursive procedures. Introduction of for loop with step – very general. The switch.
months
For days := 31, 28, 31, 30, 31, 31, 31, 30, 31, 30 do
For days := 31, if (mod(year, 4) = 0 then 29, else 28, 31, 30, 31, 31, 31, 30, 31, 30
Homework: Print Oscillating sum
Homework: Set up Prolog
Data types:
Early on, model linked list, binary tree, with arrays. Think. How would do it?
COBOL – allowed specification of precision, structured data type for records. PL/I – extended precision to ints and floats. ALGOL 68: primitives and structure-defining ops. (examples of ops – in C: {}, (), *, []) User defined data types – able to associate name w/ data type. Abstract data types – use of a type differs from internal representation and ops available on type
Homogeneous (array) vs. heterogenous (record).
Primitives – not based on other types. Ints reflect storage in hardware. Others – in software.
Numerics – integers: signed (one’s complement, two’s complement), unsigned, short, int, long. Floats: 1 sign bit, 8 bit exponent, 23 bit fraction = 32. Double: 1/11/52 = 64.
Decimal: use byte or nibble per digit. Decimal point does not float. Boolean types. As bit, byte, int. Char type: ASCII, Unicode (2 byte).
String Types: might be built in or built upon array of char. Do we allow array ops on it. Should they be static or dynamic length?
Not primitive: C++, Pascal, Ada.
In Ada: array of char, can reference a single char. Various ops built in.
substr: name1(2:4)
& for concatenation. As in VB6.
C++: ignoring the stl. After all, literal strings are arrays of char, null terminated. Built in library functions – strcpy, strcat, etc.
FORTRAN 70+: they are primitives. Have assignment, relational ops, concatenation, substring.
Java: primitive type. String class: holds constant strings. StringBuffer. Why this is really annoying. String comparisons in Java.
SNOBOL4, Perl, Javascript: pattern matching string op. many other langs: as functions.
In SNOBOL4, patterns can be assigned to variables.
LETTER = ‘abcdefghijklmnopqrstuvwxyz’
WORDPATTERN = BREAK(LETTER) SPAN(LETTER) . WORD
Means skip until find a letter, then span letters, then assign (the .) to the variable WORD
TEXT WORDPATTERN
Perl: Based on regular expressions. /[A-Za-z][ [A-Za-z]+/ /\d+\. ?\d* | \.\d+/
static vs. dynamic string lengths
FORTRAN 90:
CHARACTER (LEN = 15) A, B
Always full, empty chars are blank.
C, C++: limited dynamic. Except for STL
SNOBOL4, JavaScript, Perl: dynamic
Talk about benefits, drawbacks of each scheme
Implementation
Static: at compile time: name of type, the length, the address
Limited dynamic: store capacity, current length. (though C++ needs this not)
No need for dynamic allocation.
Dynamic: as linked list, but have many pointers. Dense list. But what if space afterwards is claimed – must realloc and copy. We can use a mixture of the two approaches.
User-defined Ordinals.
enum. C, Ada
Design: In Pascal, a given enum val (e.g. January) not allowed to be used in more than a single enum, cannot be input or output, but can be assigned, compared, used in for loop.
Some languages allow overloading of these literals, but then need to specify type:
e.g. type letters is (‘A’, ‘B’, ‘C’, ‘D’ ….
type vowels is (‘A’, ‘E’, ‘I’, ‘O’, ‘U’)
for letter in ‘A’ ,,. ‘U’ loop
for letter in vowels(‘A’) ,,. Vowels(‘U’) loop
Ada’s BOOLEAN and CHARACTER are predefined enums
Ops: pred, successor, position. Pascal: pred(blue) is red. Ada, as attributes: Letter’Pred(‘B’) is ‘A’
Improves readability, reliability
Subrange types – continuous subsequence of an ordinal
Pascal:
type
uppercase = ‘A’ .. ‘Z’;
index = 1 .. 100;
In Ada, called subtypes. Assuming already defined an enum:
Subtype WEEKDAYS is DAYS range Mon .. Fri
Subtype INDEX is INTEGER range 1 .. 100
Ada allows assignment from parent to subtype unless it is not defined, so might assign Tuesday but not Sunday.
Recall that diff from Ada’s type, where cannot assign from parent to derived type.
Implementation: As parent types, but with range checking for each assignment.
Array Types
Posted by
joshwaxman
at
11:55 AM
0
comments
![]()
Tuesday, February 21, 2006
Syllabus - work in progress
Work in progress - to be refined, added to, etc.
- Preliminaries
- why study programming languages, programming domains, criteria to evaluate languages, influences on language design, language categories, design trade-off.
- Some History
- pseudocodes, FORTRAN, ALGOL. discuss other languages later, as they come up.
- Syntax
- describing syntax, lexemes, tokens, language recognizers and generators, BNF and CFGs, EBNF, parse trees, ambiguity, precedence, associativity, regular expressions, FSA, NFSAs, PDAs.
- Lexical analysis, parsing, lex and yacc.
- Names, Bindings, Type Checking, Scopes, Lifetime. static and dynamic
- Data Types
- Primitives, strings, user-defined ordinals, arrays, associative arrays, records, unions, sets, pointers. Also, some discussion of ALGOL
- Expressions and Assignment statements
- arithmetics expressions, overloaded operators, type conversions, relational/boolean expressions, short circuit evaluation, assignment statements, mixed-mode assignment. More ALGOL.
- Control Structures
- compound statements, selection statements, iterative statements, unconditional branching, guarded commands
- Subprograms
- design issues, local referencing environments, parameter passing methods, overloaded subprograms, generic subprograms, separate and independent compilation, design issues for functions, accessing nonlocal environments, user-defined overloaded operators, coroutines.
- Implementing subprograms
- General semantics of calls and returns, implementing: FORTRAN subprograms, ALGOL subprograms, blocks, dynamic scoping, parameters that are subprogram names.
- Encapsulation, OOP - we will probably skip since we already know this fairly well.
- Concurrency - perhaps
- Exception handling - perhaps if have time at the end, since will cover this elsewhere
- in PL/I, in Ada, in C++, in Java
- Functional Programming - we will do LISP
- Mathematical functions, fundamentals of functional programming langs, LISP, Scheme, Common LISP, ML, Haskell, Applications of, comparison between functional and imperative languages
- Logic Programming Languages - Prolog
- Predicate Calculus, Proving Theorems, Logic Programming, Intro to Prolog, applications of
Posted by
joshwaxman
at
9:23 PM
0
comments
![]()
Bindings And Scope
3. Variables
Replace absolute address with symbols. A tuple: (name, address, value, type, lifetime, scope).
address: can have many instantiations of same name at different addresses. via functions, different scope, recursion. vs.
alias - many names for one address. EQUIVALENCE in Fortran. Pascal and Ada's variant record structure. C's union. C's pointers, C++'s references.
type - defines value range and ops can perform. unsigned short int.
value - contents of mem cell.
4. Binding
Association between attrib and entity, or between op and symbol.
binding time = when binding takes place.
int count; ... count = count + 5;
Bindings and binding times:
set of poss types for count: lang design time
type of count: compile time
poss values for count: compiler design time
count's value: execution time
meanings of +: lang definition time
meaning of + in this statement: compile time
internal representation of 5: compiler design time
binding attribs to vars: static = before runtime. vs. dynamic.
Type Binding. static w/ or w/o explicit declarations. Modern: Perl, ML - no explicit. VB6 optional. Fortran, PL/I, Basic: implicit. we spoke about Fortran's convention, and about unreliability. C: declarations vs definitions. dynamic: not bound by declaration, but at assignment, and can be reassigned. =flexibility. func can deal with data of any type. C++ needs know type of the data. Consider swap in C.
Jscript: list = [1.4, 4.5] and can reassign to a scalar.
lack of reliability due to typos generating new vars, or if assignment should not work, will.
usually interpreted rather than compiled because hard to implement dynamic type changes in machine code.
Type inference: ML can infer type.
fun circum(r) = 3.14 * r * r;
fun square(x) : int = x * x; //int specifies return type
Storage Bindings/Lifetimes
allocation/deallocation. lifetime= time var bound to a specific address.
static vars - throughout program execution. retain history, speed 'cause no alloc/dealloc. no recursion, waste of space.
stack-dynamic - allocated when declaration statement reached. could either be when enter func (Ada) or when reach that pos (Java). Allows recursion, sharing of space.
explicit heap-dynamic - using new and delete
implicit heap-dynamic - Perl, Javascript arrays and strings. as a result of assignment.
Type-Checking
For both operations and functions. Type checking: make sure operands are of compatible types. compatible = legal for operator or can be implicitly converted (=coersion). type error - where cannot apply operator to operand.
depends on bindings of vars to types. if static, can do type checking statically. if dynamic, must be done at runtime = dynamic type checking. better to detect earlier. tradeoff of reliability with flexibility. What about variants, unions? Must maintain current type, if do actually check.
Strong Typing
Structured programming in 70's --> strong typing. each name has single type, defined statically = known at compile time. For variant records: type errors are always detected.
Pascal: almost strongly typed. allows type tag omission in variants.
Ada as well: variants dynamically checked. But can specify UNCHECKED_CONVERSION function. oiwerful, useful for using pointers as ints for user-defined storage allocation/deallocation. Modula-3: LOOPHOLE
C, C++: not. functions where parameters not type-checked. Namely, the "..." How do you think printf works?
ML: Strong: types all statically known, from declarations of inference.
Java: Strongly typed. Can do explicit conversion, resulting in type error, but no implicit conversion. at least in assignment. still some implicit coversion, in terms of evaluating expressions. int + float. string + int. "hello" + i + j.
more coercion --> less reliability.
Type Compatibility
in terms of assignment, most often. name type compatibility = only if have same names.
structure type compatibility - if structures are the same.
Consider the enum in C. Can we assign it to an int of v.v.?
When pass vars to funcs. if we define locally, who is to say that types are the same? Original Pascal - define it globally.
flexibility vs. difficulty implementing. compiler compare name, or compare each element type. What if have same structure in terms of data types but diff field names? Diff subscript ranges (0...9) vs (1..10)? Two enums with same num of components?
type celsuis = real;
type fahrenheit = real;
Pascal did not initally specify, which led to diff implementations. ISO Pascal - mixed: declaration equivalence - if define one type name = another type.
Ada: derived type vs subtype. derived:
type celsuis is new FLOAT;
type fahrenheit is new FLOAT;
cannot assign to each other, to and fro FLOATS, except literals.
subtype is compatible with parent:
subtype SMALL_TYPE is INTEGER [range 0 .. 99];
C: structural equivalence.
C++: name equivalence. typedef does not introduce new type, but acts as a macro.
Ada: need no type names
C, D : array (1 .. 10) of INTEGER; is incompatible
type: LIST_10 is array (1 .. 10) of INTEGER;
C, D: LIST_10;
Scope
scope = range in which is visible, ie can be referenced in a statement. locals vs. globals.
ALGOL 60: static scope. this is what we are used to. in C: globals seen in functions. within functions, nested ifs, blocks, etc. However, also nested procedures. static parent and ancestors.
Also, have narrower scop hiding wider scope. Scope resolution op in C++. C++ doesn't allow nested funcs, but do allow globals.
procedure big;
var x : integer;
procedure sub1;
begin { sub1 }
...x...
end; {sub1}
procedure sub2;
var x : integer;
begin { sub2 }
...x...
end; {sub2}
begin { big }
...x...
end; {big}
Blocks
Again, ALGOL 60.
In Ada:
declare TEMP : integer
begin
TEMP := FIRST
FIRST := SECOND
SECOND := FIRST
end;
C, Java: {}. for's changing scope.
Dynamic Scope
APL, SNOBOL4, early lisp
problems: cannot determine attributes statically.
1) less reliable, since subprograms, even far off textually, can modify local vars.
2) cannot do static type checking
3) akin to Spaghetti code.
4) speed issues - much slower to access
benefits: no need to pass vars, bec implicitly visible
But static is more readable and faster. perhaps later discuss implementation of each.
Posted by
joshwaxman
at
5:14 PM
0
comments
![]()
Reading in ALGOL, Compiling in ALGOL
We are about ready to move on to the next programming language: ALGOL.
Here is a page with some free ALGOL compilers and interpreters. Try installing one and see if the following "hello world" code will run:
'BEGIN'Or in ALGOL 68:
'COMMENT' Hello World in Algol 60;
OUTPUT(4,'(''('Hello World!')',/')')
'END'
( # Hello World in Algol 68 # print(("Hello World!",newline)))In the book, read from pg. 95-121.
Here is a Wikipedia article on ALGOL:
Posted by
joshwaxman
at
12:30 PM
0
comments
![]()
Analysis of a FORTRAN Matrix Program - III
The code, as a reminder:
! program to calculate whether a graph is strongly connected
! it calculates this my using matrix multiplication on the
! adjacency matrix representing the graph
PROGRAM matrix
INTEGER :: length
PARAMETER (length = 4)
INTEGER :: a,b, c, m(length,length), copy(length,length), total, d, e, f
m(1, :) = (/ 1, 0, 1, 0/)
m(2, :) = (/ 1, 0, 0, 0/)
m(3, :) = (/ 1, 1, 0, 1/)
m(4, :) = (/ 0, 0, 1, 0/)
!initialize a copy of m so that we may calculate N^2
copy = m
DO a = 1, length
DO b = 1, length
total = 0
DO c = 1, length
total = m(a,c) * copy(c,b) + total
END DO
IF (total > 0) THEN
m(a,b) = 1
ELSE
m(a,b) = 0
END IF
END DO
END DO
DO f = 1, length
PRINT *, m(f,1:4)
END DO
DO e = 1, length
total = 0
DO d = 1, length
IF( m(d,e) .EQ. 1 .AND. m(e,d) .EQ. 1 ) total = total + 2
END DO
IF ( total == 8 ) THEN
PRINT *, 'Strongly Connected At: ', e
ELSE
PRINT *, 'Not Strongly Connected At: ', e
END IF
END DO
END PROGRAM matrix
Now, while the example I used in class had only 1s and 0s in the result, in reality we may have higher numbers. This is fine. A zero in position (i,j) means that there is no path from i to j, but a number greater than zero, such as 1 or 3 or 8, means that there is a path. So we need not check specifically for a nonzero and set the result to 1.
One we know this, we may use the built-in matmul function that I suggested you use, rather than doing the matrix multiplication by hand. Doing matmul it by hand is certainly still good programming exercise, but if we have this function built in, it may just be incredibly optimized. Further, it saves programmer work. Further, it makes the code smaller and thus more readable and less error-prone.
There was actually a bug in this code, which I should comment upon before proceeding:
The problem is twofold. Firstly, we are only doing a single matrix multiplication in this entire code - calculating M^2 rather than M^4. Secondly, we are not even calculating M^2 correctly! This is because we are modifying M in the middle of the multiplication! M(1,1) is being set, and then that value is being used to compute M(1,2), M(1,3), M(1,4), and M(2,1), M(3,1), and M(4,1). We could solve this by making a third matrix, result, and assigning to that matrix, and then stating m = result at the end. But let us skip this entire step and just use the built in matmul function. We no longer need the copy matrix for this purpose, but I will leave it in in case we need it for some other purpose. I will change the code, commenting out the previous code so we can see what changed. I will still only calculate M^2. We will deal with M^4 and the associated problem later.
DO a = 1, length
DO b = 1, length
total = 0
! the following code calculates a single dotproduct
DO c = 1, length
total = m(a,c) * copy(c,b) + total
END DO
! and here we assign the result to m
IF (total > 0) THEN
m(a,b) = 1
ELSE
m(a,b) = 0
END IF
END DO
END DO
! program to calculate whether a graph is strongly connected
! it calculates this my using matrix multiplication on the
! adjacency matrix representing the graph
PROGRAM matrix
INTEGER :: length
PARAMETER (length = 4)
INTEGER :: a,b, c, m(length,length), copy(length,length), total, d, e, f
m(1, :) = (/ 1, 0, 1, 0/)
m(2, :) = (/ 1, 0, 0, 0/)
m(3, :) = (/ 1, 1, 0, 1/)
m(4, :) = (/ 0, 0, 1, 0/)
!initialize a copy of m so that we may calculate N^2
copy = m
!DO a = 1, length
! DO b = 1, length
! total = 0
!
! DO c = 1, length
! total = m(a,c) * copy(c,b) + total
! END DO
!
! IF (total > 0) THEN
! m(a,b) = 1
! ELSE
! m(a,b) = 0
! END IF
! END DO
!END DO
! calculate M^2
m = matmul(m, m)
DO f = 1, length
PRINT *, m(f,1:4)
END DO
DO e = 1, length
total = 0
DO d = 1, length
IF( m(d,e) .EQ. 1 .AND. m(e,d) .EQ. 1 ) total = total + 2
END DO
IF ( total == 8 ) THEN
PRINT *, 'Strongly Connected At: ', e
ELSE
PRINT *, 'Not Strongly Connected At: ', e
END IF
END DO
END PROGRAM matrix
Posted by
joshwaxman
at
10:06 AM
0
comments
![]()
Analysis of a FORTRAN Matrix Program - II
The program already has a nice feature. It defines length to be 4 and then uses length throughout in the loops. That way, if we want to change the program to handle a 5 X 5 matrix, we can just change the declaration of our matrices to 5 X 5, and length to = 5, and the program will run. Using symbols instead of literals in this way makes the program mode readily adaptable.
The program, again:
! program to calculate whether a graph is strongly connected
! it calculates this my using matrix multiplication on the
! adjacency matrix representing the graph
PROGRAM matrix
INTEGER :: a,b, c, m(4,4), copy(4,4), total, length = 4, d, e, f
m(1, :) = (/ 1, 0, 1, 0/)
m(2, :) = (/ 1, 0, 0, 0/)
m(3, :) = (/ 1, 1, 0, 1/)
m(4, :) = (/ 0, 0, 1, 0/)
! copy(1, :) = (/ 1, 0, 1, 0/)
! copy(2, :) = (/ 1, 0, 0, 0/)
! copy(3, :) = (/ 1, 1, 0, 1/)
! copy(4, :) = (/ 0, 0, 1, 0/)
!initialize a copy of m so that we may calculate N^2
copy = m
DO a = 1, length
DO b = 1, length
total = 0
DO c = 1, length
total = m(a,c) * copy(c,b) + total
END DO
IF (total > 0) THEN
m(a,b) = 1
ELSE
m(a,b) = 0
END IF
END DO
END DO
DO f = 1, length
PRINT *, m(f,1:4)
END DO
DO e = 1, length
total = 0
DO d = 1, length
IF( m(d,e) .EQ. 1 .AND. m(e,d) .EQ. 1 ) total = total + 2
END DO
IF ( total == 8 ) THEN
PRINT *, 'Strongly Connected At: ', e
ELSE
PRINT *, 'Not Strongly Connected At: ', e
END IF
END DO
END PROGRAM matrix
However, as implemented, there are two things I would change. Firstly, length is declared as a variable. This means that somewhere in the program, I might change it by accident. It would be better to declare it a constant. But how do we do this in FORTRAN? The answer, we declare its data type and then set its value with a PARAMETER statement.
Another thing I would change: the declaration of our matrices m and copy use a literal 4. When modifying the program, I would not only have to change the definition of length but my matrix definitions as well. Instead, let us use our new constant to define the matrix size. We will also remove the old code that was commented out:
! program to calculate whether a graph is strongly connected
! it calculates this my using matrix multiplication on the
! adjacency matrix representing the graph
PROGRAM matrix
INTEGER :: length
PARAMETER (length = 4)
INTEGER :: a,b, c, m(length,length), copy(length,length), total, d, e, f
m(1, :) = (/ 1, 0, 1, 0/)
m(2, :) = (/ 1, 0, 0, 0/)
m(3, :) = (/ 1, 1, 0, 1/)
m(4, :) = (/ 0, 0, 1, 0/)
!initialize a copy of m so that we may calculate N^2
copy = m
DO a = 1, length
DO b = 1, length
total = 0
DO c = 1, length
total = m(a,c) * copy(c,b) + total
END DO
IF (total > 0) THEN
m(a,b) = 1
ELSE
m(a,b) = 0
END IF
END DO
END DO
DO f = 1, length
PRINT *, m(f,1:4)
END DO
DO e = 1, length
total = 0
DO d = 1, length
IF( m(d,e) .EQ. 1 .AND. m(e,d) .EQ. 1 ) total = total + 2
END DO
IF ( total == 8 ) THEN
PRINT *, 'Strongly Connected At: ', e
ELSE
PRINT *, 'Not Strongly Connected At: ', e
END IF
END DO
END PROGRAM matrix
Posted by
joshwaxman
at
9:45 AM
0
comments
![]()
Analysis of a FORTRAN Matrix Program - I
Here I present a matrix homework. I will post comments and suggestions in a series of posts. First, here is the program at the outset.
PROGRAM matrix
INTEGER :: a,b, c, m(4,4), copy(4,4), total, length = 4, d, e, f
m(1, :) = (/ 1, 0, 1, 0/)
m(2, :) = (/ 1, 0, 0, 0/)
m(3, :) = (/ 1, 1, 0, 1/)
m(4, :) = (/ 0, 0, 1, 0/)
copy(1, :) = (/ 1, 0, 1, 0/)
copy(2, :) = (/ 1, 0, 0, 0/)
copy(3, :) = (/ 1, 1, 0, 1/)
copy(4, :) = (/ 0, 0, 1, 0/)
DO a = 1, length
DO b = 1, length
total = 0
DO c = 1, length
total = m(a,c) * copy(c,b) + total
END DO
IF (total > 0) THEN
m(a,b) = 1
ELSE
m(a,b) = 0
END IF
END DO
END DO
DO f = 1, length
PRINT *, m(f,1:4)
END DO
DO e = 1, length
total = 0
DO d = 1, length
IF( m(d,e) .EQ. 1 .AND. m(e,d) .EQ. 1 ) total = total + 2
END DO
IF ( total == 8 ) THEN
PRINT *, 'Strongly Connected At: ', e
ELSE
PRINT *, 'Not Strongly Connected At: ', e
END IF
END DO
END PROGRAM matrix
One thing that is missing from this program is comments. Tell me what the program is supposed to do, and what each section of the code is supposed to do. It used to be that the letter C at the beginning of the line would start a comment. Here, instead, we use the character !
Another thing to realize is that you can assign an entire matrix to another matrix with the = operator. You need not initialize copy separately, or even loop, copying elements. Rather, just use =. I will comment out the code and put in the new code in its place. My changes in red.
! program to calculate whether a graph is strongly connected
! it calculates this my using matrix multiplication on the
! adjacency matrix representing the graph
PROGRAM matrix
INTEGER :: a,b, c, m(4,4), copy(4,4), total, length = 4, d, e, f
m(1, :) = (/ 1, 0, 1, 0/)
m(2, :) = (/ 1, 0, 0, 0/)
m(3, :) = (/ 1, 1, 0, 1/)
m(4, :) = (/ 0, 0, 1, 0/)
! copy(1, :) = (/ 1, 0, 1, 0/)
! copy(2, :) = (/ 1, 0, 0, 0/)
! copy(3, :) = (/ 1, 1, 0, 1/)
! copy(4, :) = (/ 0, 0, 1, 0/)
!initialize a copy of m so that we may calculate N^2
copy = m
DO a = 1, length
DO b = 1, length
total = 0
DO c = 1, length
total = m(a,c) * copy(c,b) + total
END DO
IF (total > 0) THEN
m(a,b) = 1
ELSE
m(a,b) = 0
END IF
END DO
END DO
DO f = 1, length
PRINT *, m(f,1:4)
END DO
DO e = 1, length
total = 0
DO d = 1, length
IF( m(d,e) .EQ. 1 .AND. m(e,d) .EQ. 1 ) total = total + 2
END DO
IF ( total == 8 ) THEN
PRINT *, 'Strongly Connected At: ', e
ELSE
PRINT *, 'Not Strongly Connected At: ', e
END IF
END DO
END PROGRAM matrix
Posted by
joshwaxman
at
9:31 AM
0
comments
![]()
Monday, February 20, 2006
Some Pointers with the FORTRAN matrix assignment
1)
Definition of Strongly Connected Graph
A directed graph is called strongly connected if for every pair of vertices u and v there is a path from u to v and a path from v to u.2) A program that uses the built in matmul, and does assignment from one matrix to another:
! EXAMPLE 4
!
! Aprogram to compute the largest eigenvalue
! of a real, dense matrix by the power method
integer, parameter::devno=10, n=10, minit = 10, maxit=100
real::lambda_old, lambda_new
real::rel_err, tol = 2.0**(-20)
real,dimension(n)::x_new, x_old=(/(1.0/n,i=1,n)/)
real,dimension(n,n)::a
open(devno, file='a.dat')
read(10,10) ((a(i,j),j=1,n),i=1,n)
10 format(10f4.1)
iterate: do i=1,maxit
write (*,*) "i = ", i
x_new=matmul(a, x_old)
lambda_new = sqrt(dot_product(x_new, x_new))
write(*,*) "lambda_new = ", lambda_new
if (i .gt. minit) then
rel_err = abs((lambda_new - lambda_old)/lambda_old)
if (rel_err .lt. tol) exit iterate
endif
if (i .eq. maxit) write (*,*) "Maximum Iterations reached"
lambda_old = lambda_new
x_old = x_new/lambda_new
end do iterate
write(*,*) "lambda = ", lambda_new
end
Another place that uses matmul.
Posted by
joshwaxman
at
2:59 PM
0
comments
![]()
Friday, February 17, 2006
Explaining Lex and Yacc
Note: Change {} after includes to pointy brackets.
1)
What exactly are you doing when you process something with lex?
Well, lex takes your lex file, say example2.l and generates a file in the C language. The name of this file is lex.yy.c.
In class, I spoke about Finite State Machines, and how they can recognize regular languages. lex.yy.c is an implementation of a Finite State Machine based on your lex file. The regular expressions are inputs, and the actions or printfs are the outputs.
Thus, let us say we have example2.l:
%{
#include {stdio.h}
%}
%%
[0123456789]+ printf("NUMBER\n");
[a-zA-Z][a-zA-Z0-9]* printf("WORD\n");
%% The stuff between %{ and %} will be included in the C file, which is important since we are using printf. The stuff between %% and %% are regular expressions together with the action to take after successfully recognizing that expression.At the command line, we type:
lex example2.l
This generates the file lex.yy.c.
Pseudocode to explain what this file contains (obtained from this website):
state= 0; get next input characterThus, we start at the start state, read input. So long as we are matching, we calculate a new state based on current state and input character. We do this until we enter an accept state. If we do, we go to the start state once again, so we can match the next string (=token), . If we go to an error state along the way, we say so and try matching again.
while (not end of input) {
depending on current state and input character
match: /* input expected */
calculate new state; get next input character
accept: /* current pattern completely matched */
state= 0; perform action corresponding to pattern
error: /* input unexpected */
state= 0; echo 1st character input after last accept or error;
reset input to 2nd character input after last accept or error;
}
We need not go into detail here how exactly lex.yy.c implements this Finite State Machine in C. You can try examining the code if you want.
Now, if we want to run this Finite State Machine in lex.yy.c, we cannot, because it is written in C, not in machine language. Thus, we must compile the file.
There are two ways to compile it. We can incorporate the lex.yy.c with other files in a C project, and call the various functions and access the variables it exposes. We would need to do this because lex.yy.c does not have its own main function. Alternatively, we could specify that libl provide us with an appropriate main(). We do the latter.
Thus, at the command line, we type:
cc lex.yy.c -o example2 -ll
This -ll gets the main() function from libl. -o states that the output file should be what we specify, namely example2.
We can then run the executable, example2.
2) What exactly does yacc do?
yacc takes a yacc file which contains BNF and generates a C file which implements a Push Down Automaton (PDA) which accepts the context free language specified in the yacc file.
We use yacc together with lex.
Our lex file will recognize and inform us about tokens, while our yacc file will base itself upon those tokens and recognize a context free grammar.
Beforehand, we used the -ll option with the cc command, so that we were provided with a main() function.
Now, however, we want to compile more than just the lex.yy.c file. We want to incorporate it with C code generated by yacc. Thus, we will no longer use the -ll option. Instead, we will make sure that our yacc file has a main() function defined.
3)
Let us consider example4, which is the thermostat example.
Create a lex file, example4.l. The contents of this file should be:
Most of this should be familiar. We are matching tabs, newlines, the string "on" or "off", etcetera.%{
#include {stdio.h}
#include "y.tab.h"
%}
%%
[0-9]+ return NUMBER;
heat return TOKHEAT;
on|off return STATE;
target return TOKTARGET;
temperature return TOKTEMPERATURE;
\n /* ignore end of line */;
[ \t]+ /* ignore whitespace */;
%%
One thing is different, though. Rather that just having #include {stdio.h}, we have an additional line that we are explicitly marking to be included in the generated C file, lex.yy.c. That line is:
#include "y.tab.h"y.tab.h is a header file needed in association with the C file generated by yacc, namely y.tab.c.
We now need a yacc file. The tutorial does a bad job here by separating parts of the file, and not . Basically, we need a single file that does three things:
- Provide literal code that will include necessary .h files and provide needed functions such as main(). This part will be between %{ and %}
- Give a definition of the tokens to be used in our grammar. This line will start %token.
- Lay out the context free grammar, with rules, as well as actions to take (such as printf) after the rule has been satisfied. This should be embedded within %% and %% tags, but the tutorial omitted it, and thus you may have had a compile time error.
%{Save this file as example4.y. Then run yacc on it by typing at the command line:
#include
#include
void yyerror(const char *str)
{
fprintf(stderr,"error: %s\n",str);
}
int yywrap()
{
return 1;
}
main()
{
yyparse();
}
%}
%token NUMBER TOKHEAT STATE TOKTARGET TOKTEMPERATURE
%%
commands: /* empty */
| commands command
;
command:
heat_switch
|
target_set
;
heat_switch:
TOKHEAT STATE
{
printf("\tHeat turned on or off\n");
}
;
target_set:
TOKTARGET TOKTEMPERATURE NUMBER
{
printf("\tTemperature set\n");
}
;
%%
yacc example4.y
This will generate two files, y.tab.h and y.tab.c.
Now, we have our three files:
lex.yy.c
y.tab.c
y.tab.h
We need to compile them. Remember we are not using the -ll option since we are providing our own main() function.
cc lex.yy.c y.tab.c -o example4Then run example4.
Posted by
joshwaxman
at
11:22 AM
1 comments
![]()
Thursday, February 16, 2006
Names and Binding
We may return to talk more about parsing later.
1. Name forms:
max length, connector characters, case sensitivity, Limitation on max length to ease symbol table. C++ unlimited, but depends on implementation. does case sensitivity hurt readability, reliability, writability?
2. Special words = keywords vs. reserved words.
REAL APPLE
REAL = 3.4
INTEGER REAL
REAL INTEGER
predefined names in Ada. INTEGER and FLOAT are there by default but may be overridden. Pascal. Others in Ada brought in via with statements. printf and scanf in C.
3. Variables
Replace absolute address with symbols. A tuple: (name, address, value, type, scope).
address: can have many instantiations of same name at different addresses. via functions, different scope, recursion. vs.
alias - many names for one address. EQUIVALENCE in Fortran. Pascal and Ada's variant record structure. See here: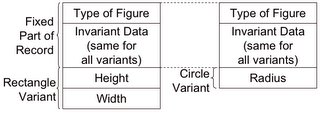 How do we implement this? Change size of allocate maximum.
How do we implement this? Change size of allocate maximum.
constrained vs. unconstrained.
TYPE Geom_Type IS (Unknown, Rectangle, Circle);
TYPE Geometric_Figure(Figure_Type : Geom_Type := Unknown) IS RECORD
-- Invariant data fields here
CASE Figure_Type IS
WHEN Rectangle =>
Width : Float;
Height : Float;
WHEN Circle =>
Radius : Float;
WHEN Unknown =>
NULL;
END CASE;
END RECORD;
-- An unconstrained Geometric_Figure
GC : Geometric_Figure( Figure_Type => Circle );
-- A constrained Geometric Figure of Figure_Type Circle
discriminant, fixed, variant. reading allowed for all, var so long as proper type. writing: discr if dont change val or as record assignment. record assignment allowed if unconstrained, else discr must match. record compare if discr match/
C's union. C's pointers, C++'s references.
type - defines value range and ops can perform. unsigned short int.
value - contents of mem cell.
4. Binding
Association between attrib and entity, or between op and symbol.
binding time = when binding takes place.
int count; ... count = count + 5;
Bindings and binding times:
set of poss types for count: lang design time
type of count: compile time
poss values for count: compiler design time
count's value: execution time
meanings of +: lang definition time
meaning of + in this statement: compile time
internal representation of 5: compiler design time
binding attribs to vars: static = before runtime. vs. dynamic.
Type Binding. static w/ or w/o explicit declarations. Modern: Perl, ML - no explicit. VB6 optional. Fortran, PL/I, Basic: implicit. we spoke about Fortran's convention, and about unreliability. C: declarations vs definitions. dynamic: not bound by declaration, but at assignment, and can be reassigned. =flexibility. func can deal with data of any type. C++ needs know type of the data. Consider swap in C.
Jscript: list = [1.4, 4.5] and can reassign to a scalar.
lack of reliability due to typos generating new vars, or if assignment should not work, will.
usually interpreted rather than compiled because hard to implement dynamic type changes in machine code.
Type inference: ML can infer type.
fun circum(r) = 3.14 * r * r;
fun square(x) : int = x * x; //int specifies return type
Storage Bindings/Lifetimes
allocation/deallocation. lifetime= time var bound to a specific address.
static vars - throughout program execution. retain history, speed 'cause no alloc/dealloc. no recursion, waste of space.
stack-dynamic - allocated when declaration statement reached. could either be when enter func (Ada) or when reach that pos (Java). Allows recursion, sharing of space.
explicit heap-dynamic - using new and delete
implicit heap-dynamic - Perl, Javascript arrays and strings. as a result of assignment.
Posted by
joshwaxman
at
5:03 PM
0
comments
![]()
Some Linear Algebra
Dot Product
1x + 3y + 7z = 7
[1 3 7] · [x y z] = 7
scalar result. transpose.
Solving sets of Linear equations. n equations and n unknowns
x + 4y + 6z = 6
2x + 5y + 15z = -1
2x + 5y = 9
Matrix multiplication. Can implement various operations. Swap rows, add multiple of one row to another, etc.
[1 4 6] [x] [ 6 ]
[2 5 15] X [y] = [-1 ]
[2 5 0] [z] [ 9 ]
Other matrix ops: multiplication by a scalar. matrix addition.
Matrix multiplication, addition, useful for finding cyles in graphs.
Adjacency matrix. A X A yields all cycles of length 2 in the diagonal.
An yields all cycles of length n.
A + A2 + A3 + ... An. Looking at one full row or column will tell us if the graph is strongly connected.
Posted by
joshwaxman
at
12:44 PM
0
comments
![]()
Tuesday, February 14, 2006
Definitions: Finite State Machines
The wikipedia entry on Finite State Machines, which breaks down into Deterministic and Nondeterministic finite state machines. Read up to and including the section on Acceptors and Recognizers, and Figure 2. Skip transducers if you wish, and read the mathematical model for acceptors.
If you want to read about PDAs, see here.
If you want, you can read about Turing Machines.
Posted by
joshwaxman
at
5:55 PM
0
comments
![]()
Linear Algebra: Definition of Matrix Multiplication
Read this wikipedia article, up to but not including the section labelled the proportions-vectors method.
I hope to explain all this at the bigeinning of next class.
Posted by
joshwaxman
at
5:05 PM
0
comments
![]()
Linear Algebra: Definition of Dot Product
From wikipedia:
In mathematics, the dot product, also known as the scalar product, is a binary operation which takes two vectors and returns a scalar quantity. It is the standard inner product of the Euclidean space.
The dot product of two vectors a = [a1, a2, … , an] and b = [b1, b2, … , bn] is by definition
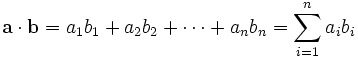
where Σ denotes summation notation. For example, the dot product of two three-dimensional vectors [1, 3, −2] and [4, −2, −1] is
- [1, 3, −2]·[4, −2, −1] = 1×4 + 3×(−2) + (−2)×(−1) = 0.
Using matrix multiplication and treating the row vectors as 1×n matrices, the dot product can also be written as
where bT denotes the transpose of the matrix b. Using the example from above, this would result in a 1×3 matrix (i.e. vector) multiplied by a 3×1 vector (which, by virtue of the matrix multiplication, results in a 1×1 matrix):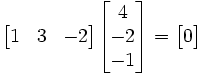
Posted by
joshwaxman
at
4:59 PM
0
comments
![]()
Monday, February 13, 2006
A bit on regular expressions
From wikipedia:
Regular expressions consist of constants and operators that denote sets of strings and operations over these sets, respectively. Given a finite alphabet Σ the following constants are defined:
- (empty set) ∅ denoting the set ∅
- (empty string) ε denoting the set {ε}
- (literal character) a in Σ denoting the set {a}
and the following operations:
- (concatenation) RS denoting the set { αβ | α in R and β in S }. For example {"ab", "c"}{"d", "ef"} = {"abd", "abef", "cd", "cef"}.
- (alternation) R|S denoting the set union of R and S.
- (Kleene star) R* denoting the smallest superset of R that contains ε and is closed under string concatenation. This is the set of all strings that can be made by concatenating zero or more strings in R. For example, {"ab", "c"}* = {ε, "ab", "c", "abab", "abc", "cab", "cc", "ababab", ... }.
The above constants and operators form a Kleene algebra.
Many textbooks use the symbols ∪, +, or ∨ for alternation instead of the vertical bar.
To avoid brackets it is assumed that the Kleene star has the highest priority, then concatenation and then set union. If there is no ambiguity then brackets may be omitted. For example, (ab)c is written as abc and a|(b(c*)) can be written as a|bc*.
Examples:
- a|b* denotes {ε, a, b, bb, bbb, ...}
- (a|b)* denotes the set of all strings consisting of any number of a and b symbols, including the empty string
- b*(ab*)* the same
- ab*(c|ε) denotes the set of strings starting with a, then zero or more bs and finally optionally a c.
- ((a|ba(aa)*b)(b(aa)*b)*(a|ba(aa)*b)|b(aa)*b)*(a|ba(aa)*b)(b(aa)*b)* denotes the set of all strings which contain an even number of bs and an odd number of as. Note that this regular expression is of the form (X Y*X U Y)*X Y* with X = a|ba(aa)*b and Y = b(aa)*b.
The formal definition of regular expressions is purposefully parsimonious and avoids defining the redundant quantifiers ? and +, which can be expressed as follows: a+= aa*, and a? = (ε|a). Sometimes the complement operator ~ is added; ~R denotes the set of all strings over Σ that are not in R. The complement operator is redundant: it can always be expressed by only using the other operators.
Regular expressions in this sense can express exactly the class of languages accepted by finite state automata: the regular languages. There is, however, a significant difference in compactness: some classes of regular languages can only be described by automata that grow exponentially in size, while the length of the required regular expressions only grow linearly. Regular expressions correspond to the type 3 grammars of the Chomsky hierarchy and may be used to describe a regular language.
Posted by
joshwaxman
at
6:45 AM
0
comments
![]()
Sunday, February 12, 2006
BNF in the book
BNF is mentioned briefly in chapter 3, on page 96, in the book, and is described in greater detail in chapter 4, pgs 148-156
Posted by
joshwaxman
at
6:16 AM
0
comments
![]()
Wednesday, February 08, 2006
Class IV: Describing Syntax - BNF
Formal definition of the syntax.
Why?
1) feedback cycle in language formation
2) implementors of compilers/interpreters
3) users of language
syntax = form of the language, vs. semantics = meaning of language
syntax of if:
if ({expr}
but this tells us nothing about semantics.
ALGOL difficulties.
Describing Syntax:
1) Languages (natural and programming) are sets of strings of chars from an alphabet. These strings are sentences or statements. Syntax rules: which sentences are in the language.
Formal descriptions often don't deal with basic parts - lexemes, which might be specified by a separate lexical specification. Lex vs. Yacc. Lexemes: identifiers, literals, ops, keywords. programs = string of chars, or string of lexemes.
token = category of its lexemes. the output of Lex.
identifier might be total, count, etc..
plus_op just has + as the literal
index = 2 * count + 17;
Q: what are the tokens, what are the lexemes?
2) Two ways of defining lang: lang recognizer vs. lang generator. R (recognizer) takes in input and tells if it valid program. G generates all possible programs. These are related problems.
3) Formal methods of Describing Syntax:
BNF - Backus Naur Form. related to Chomsky's context free grammars, in context of natural language. ALGOL 58, ALGOL 60. Panini to describe Sanskrit.
series of rules, productions.
Alas, the limits of blogspot. {} instead of pointy brackets.
terminals vs. nonterminals. capital vs. lowercase. BNF grammar = collection of rules.
| for "or." Pascal:
|
use recursion to describe lists:
Start symbol S, {program}. Sentence generation called derivation.
{program} -> begin {statement_list} end
{statement_list} -> {statement} | {statement} ; {statement_list}
{statement} -> {var} = {expression}
{var} -> A | B | C
{expression} -> {var} + {var} | {var} - {var} | {var}
show derivation for begin A = B + C; B = C end
derivation order matters not, but this common approach is leftmost derivation.
HW: To implement such a grammar in C++ using STL and rand function, of by labelling rules.
Simple Grammar for Assignment:
{assign} -> {id} = {expr}
{id} -> A | B | C
{expr} -> {id} + {expr} | {id} * {expr} | ( {expr} ) | {id}
show derivation for A = B * (A+C)
4) Parse trees
show parse tree for above. parse tree matches a derivation.
5) Ambiguity
An ambiguous grammar:
{assign} -> {id} = {expr}
{id} -> A | B | C
{expr} -> {expr} + {expr} | {expr} * {expr} | ( {expr} ) | {id}
without using parentheses, what is the meaning of A = B + C * A?
Two parse trees, one with the first expansion of {expr} being the *, the other with the first being the +. Lower down in the tree, the higher its precedence.
No way to uniquely define the meaning of the structure.
6) Operator precedence:
An unambiguous grammar.
First, simple, example where went to {id} was unambiguous, but wrong precedence. Rightmost is lowest in tree, thus highest precedence.
Solution:
{assign} -> {id} = {expr}
{id} -> A | B | C
{expr} -> {expr} + {term} | {term}
{term} -> {term} * {factor} | {factor}
{factor} -> ({expr}) | {id}
show derivation of A = B + C * A on board, and simultaneously draw parse tree.
7) Associativity.
A = B + C + A
does grouping, ordering matter? Based on prev grammar, would do B + C at lowest level, first. Does in cases of large floats with limited precision. Using our unambiguous grammar, we get a left associative interpretation. (Right associative not possible because we do not have {expr} going into two {expr}s. Left associative because recursion all the way to the left. Left recursive. Can make right recursive and thus right associative.
e.g.
{factor} --> {expr} ** {factor} | {expr}
{expr} --> ({expr}) | {id}
Unambiguous if-else
look at if-else definition above. if have {statement} -> {if_statement}, ambiguity. example in C. show the two parse trees. can require begin and end
an unambiguous grammar:
the rule is that an else is matched with nearest previous unmatched then.
{statement} -> {matched} | {unmatched}
{matched} -> if {logic_expr} then {matched} else {matched} | any non-if statement
{unmatched} -> if {logic_expr} then {statement} |
if {logic_expr} then {matched} else {unmatched}
EBNF
{selection} -> if ({expr} ) {statement} [else {statement} ]
brackets for optional component rather than |. Optional recurring via actual curly braces, rather than using recursion:
{ident_list} -> {identifier} {{identifier}}
place options in non-terminal parentheses and separate via |.
Some allow number after right } to indicate upper limit on repetitions, or + to mean 1+.
Posted by
joshwaxman
at
9:06 PM
0
comments
![]()
LEX and YACC tutorial.
regular expressions and context free grammars
Posted by
joshwaxman
at
11:19 AM
0
comments
![]()
Tuesday, February 07, 2006
Passing Subroutines to Other Subroutines in FORTRAN
I hope to mention this in class today. Here is a discussion of how to.
The old-fashioned, non-profile-safe way:
SUBROUTINE SUB (ACTION)
EXTERNAL ACTION
* ...
CALL ACTION (arguments)
* ...
END
SUBROUTINE DEED (args)
* ...
END
EXTERNAL DEED
CALL SUB (DEED)
Posted by
joshwaxman
at
11:59 AM
0
comments
![]()
Wednesday, February 01, 2006
Class II - Some Early History - Pseudocodes and FORTRAN
Machine Code:
benefits: fast
drawback: hard to write. ADD might be 14. Readability. Absolute addressing. Recomputing locations, NOPs for deletions. Gave rise to Assembler, with same benefit.
issues:
floats were simulated. indexing missing - adding var quantity to fixed address.
instead, bec of the von Neumann architecture, since the instruction was in memory, they modified the address portion of the instruction, which was error prone.
thus, subroutines to do floats, and to index. since most of time spent simulating floats, little overhead comparatively for doing other things. Thus, pseudocode interpreters were natural developement.
Short Code
Words are 72 bits, as 12 6-bit bytes. mathematic expressions to be evaluated. Byte-pair values. Some codes:
01 - 06 abs 1n (n+2)nd powerimplemented as pure interpreted. 50X slower than machine code.
02 ) 07 + 2n (n+2)nd root
03 = 08 pause 4n if <= n
04 / 09 ( 58 print and tab
X0 = SQRT(ABS(Y0))
00 X0 03 20 Y0
Homework: How would we write Z0 = CUBEROOT(Y1 * Z0)? How would we write Z0=Y0?
pseudocode - generally used today as english description of code, not always going into specifics of implementation. here, means something else: an instruction diff than that provided by the machine. initially presented as way of saving space in memory, since pseudocode more compact.
Implemented a virtual computer, with own data types and operations, atop an actual computer.
Automation Principle: Automate mechanical, tedious, error-prone activities.
Also, simpler to understand since fewer exceptions, thus Regularity principle: Regular rules, w/o exceptions, are easier to read, learn, describe, implement.
Compiling routines mentioned in book are predecessor to macros.
Book designs a pseudocode, based on following capabilities:
float arithmetic and comparison, indexing, transfer of control, IO.
Syntax: Use numbers since many did not have alphabetic IO, 1 number on each card, each instruction one word. Choose how big addresses to be. Machine has only 2000 locations, so allow 3 decimal digits, and other 1000 for interpreter and program.
Impossible error Principle: rather than detecting errors, may them impossible to commit.
Since address is 3 digits and word is 10 digits, restricted to refer to 3 variables (mem locations), so commands of the form
operator operand1 operand2 dest. +1 means ADD
+1 010 150 200
Orthogonality Principle: they use + and - sign to denote reverse operations. +/-, */ divide, square/squareroot. Two orthogonal, or indep mechanisms: the number = operation, and sign=direct or reverse. two primitives combine in various ways. corollary of regularity principle.
Less to remember.
But orthogonality can go to far.
Similarly, = vs !=, and >= vs <. Need not reverse since just reverse order of operands. no need for positive, negative, zero tests. Can adopt convention that 000 contains 0. Moving: could be implemented via adding to 0, but adding floats is slow. (So do check if adding to 0 and make that a move op!) Chose 0 so that ops have easy to remember vals: move, add, multiply, square. regularity principle. Indexing and loops: x[i] -> z; x -> y[i]
+6 xxx iii zzz
-6 xxx yyy iii
Abstract out code common to all loops. Abstraction principle, corollary of Automation principle. eliminates possible source of error. "Avoid requiring something be stated more than once, factor out recurring pattern."
+7 iii nnn ddd
i = index; n=upper bound; d=location of beginning of loop. this is a do loop.
+8: read. -8 print
+9: stop
memory cards read in program as well as initial data, separated by 10 9's.
pg 20 has sample program.
Construct an interpreter for pseudocode.
read-execute cycle: called fetch-execute cycle before.
decoding by extracting their parts. similar to lexical parsing.
dest := abs(instruction) mod 1000
then, based on sign and instruction:
if sign is + then
do case op of:
0: move;
1: add;
...
if sign is - then
do case op of
0: // op if have negative 0
1: subtract;
etc.
Computational instructions:
multiply:
data[dest] := floating_product(Data[operand1], Data[operand2])
Test equality:
if floating equality (Data[operand1], Data[operand2]) then IP:=dest
Debugging:
Add to fetch-execute cycle a print of IP and the contents at IP
Statement Labels
As mentioned above, inserts into code shifts everything over.
Labeling Principle: Do not require the user to know absolute pos of item in a list, but rather associate labels with any pos that must be referenced elsewhere.
-7 0LL 000 000
this binds a symbolic label to absolute position.
Thus, equality test becomes
+4 xxx yyy 0LL
but then end up scanning program for the labels. can make label table instead.
By extension, symbol table for vars. In the data section:
+0 sss nnn 000
+d ddd ddd ddd
+0 666 150 000
+0 000 000 001
inits a 150 num array to 1s
This binds the symbol to the location at load time. And loader takes care of storage allocation, instead of having to initialize them all via cards like in the past.
+6 666 111 222
V222 := V666[V111]
Can check type info in symbol table to avoid out of bound errors.
Security Principle:
No prog that violates the def of language or intended structure should escape detection.
Extend to symbolic pseudo-code. Symbols for vars, ops.
To allow symbolic, look up ops and vars on symbol table and replace them with actual values, and then interpret. (Alteratively, could have interp directly.) Thus, first translation then interpretation.
In sum, pseudocodes provide virtual computer, which was more regular and at a higher level. Increased security, allow debugging such as traces (and breakpoints).
FORTRAN
And the IBM 704.
The engineer-coder bottleneck. On other hand, speed of execution an issue.
The IBM 704 developed together with the language, thus tightly integrated. IBM 704 supported floats directly, so no need for simulation, thus speed issue against pseudocodes, thus compiled language.
Skip features in language which not quickly produced in hardware. Thus, limits on statements, on control structures, no recursion.
FORTRAN 0: A design document. spoke of efficiency of machine code with ease of pseudocode. "FORTRAN would elim coding errors, thus little syntax error checking."
Environment: Computers slow, small, unreliable. Used primarily of scientific applications. No existing efficient way to program computers. High cost of computers vs. programmers.
FORTRAN I: Implementation introducing realities. Features: IO formatting, var names 6 chars, user defined subroutines, weird mathematical IF statement. DO Loop.
From Wikipedia:
10 dim i
20 i = 0
30 i = i + 1
40 if i <> 10 then goto 90
50 if i = 10 then goto 70
60 goto 30
70 print "Program Completed."
80 end
90 print i & " squared = " & i * i
100 goto 30
Here is the same code written using control structures.
dim i
for i = 1 to 10
print i & " squared = " & square(i)
next
print "Program Completed."
function square(i)
square = i * i
end function
No > in charset, 704 had 3 way mathematic branch instruction, which replaced FORTRAN 0's IF.
IF (arithmetic expression) N1, N2, N3
DO Loop. Was posttest rather than pretest because of 704's architecture, as well as other control statements.
No data typing. I_, J_, K_, L_, M_ are ints, rest are floats. because of scientific domain.
largest part of time spent developing spend optimizing.
FORTRAN II:
besides other features, independent compilation of subs. otherwise would crash before compiling, limiting programs to 300 - 400 lines.
FORTRAN IV:
Explicit type declarations. Why is this important? reduce errors by type checking, do not introduce new vars erroneously, expand set of names.
Logical IF construct.
Pass subs as parameters to subs.
How would we do this in C++? Digression into complex declarations in general.
Homework Assignment to print above avg nums in array.
A web site about development of FORTRAN - what features were added.
FORTRAN 77: adds char string handling, logical loop control statements (rather than just for loops), IF with optional ELSE.
FORTRAN 90: major differences. names up to 31 chars. ! as comment. collection of matrix functions: e.g. MATMUL, DOTPRODUCT, TRANSPOSE, MAXVAL, MINVAL, PRODUCT, SUM. User defined data type called "derived type." Dynamic allocation of these types, and dynamic allocation and deallocation of arrays. Vs. prev. only had static data. Select case. Exit = break, cycle = continue of C; recursion. Modules (with public and private data and methods). specification of numeric precision, ";" as statement separator. Lines up to 132 chars in length.
While array processing: A= B*Sin(A)
deprecating features.
FORTRAN 95: Minor changes. Forall, initialization of pointers, and of "derived types."
Also, NULL function, automatic garbage collection.
FORTRAN 2003:
Interop with C, international - allow , or . for decimal point. Access to command line arguments, environmental vars, procedure pointers, IO enhancements, OOP support, parameterized derived types, etc.
Some linear algebra and graph algorithm introduction. Describe the algorithm.
Next Time: Names and Binding, in more than just FORTRAN.
Posted by
joshwaxman
at
11:44 AM
0
comments
![]()
Class II - Some FORTRAN Basics - Assignment
This ftp site has a bunch of demo Fortran programs. For each Fortran file I specify, read each program to get a feel for what it does, and then copy the text of the file, compile it, and execute it.
In each case, not every line is indented 6 spaces, so either make sure that each line is indented at least 6 spaces, or else save as *.f90. Otherwise, you will get a syntax error.
1) A Kind is an integer specification of data type for primitives, in general matching the sizeof the data type in bytes. Read this webpage for more details.
Compile and run this program.
2) Data types can be defined with the keyword TYPE. Members can be accessed with %.
Compile and run this program, which creates and uses a derived type for intervals. As requested in the comment, change the program so that it prints the interval length instead.
Compile and run this program which demonstrates nested types.
3) Pointers:
Read this document about FORTRAN pointers and array pointers. Then, compile and run this program. Modify the program as suggested in the comments and see what happens.
4) Do Loop and Cycle
This example demonstrates a do loop, equivalent to a for loop. Cycle is the equivalent of continue in C++.
5) Nested do loops with names, in this example.
Exit is equivalent to break. Note that we can break out of multiple levels of loop because of the named loops. This is similar to the labelled breaks in Java.
6) Select Case statement, as we have in VB6. Note this case statement works for ranges. Example here and here.
7) Functions.
Example here. Note that just as in C, the types of parameters are not specified in the declaration, but just the names. The types are specified subsequently. LOGICAL means boolean. Note the INTENT keyword, which is used to specify that these parameters are being passed in but not out of the program. Note that the function name is also assigned a type, = to the return type, and that assigning to the function name has the effect of specifying the return value. This is also found in VB6.
8) Arrays.
Note that the : character is used to specify a range. 2:5 means 2 through 5. Either side can be optional. The , character separates indexes when dealing with a matrix. Thus, in C++:
a[7][3]
would be written a[7,3] in FORTRAN
Try out this example and compare the source with the output carefully.
9) Intended Assignments:
A) Write a program that takes N as input, reads in N numbers into an array, and prints any number A[i] which is larger than the average.
B) Take advantage of the built in matrix manipulation functions in FORTRAN to write a program that takes in N, the size of a directed graph, followed by a series of edges, terminated by -1. Compute whether the graph is strongly connected.
C) Take advantage of the full capabilities of FORTRAN 90. Write a program that will take in a series of numbers, terminates by -1, and stores them in a binary search tree. Then take another series of numbers as input and output whether the numbers are in the binary tree. (All you need implement is insert and search).
Posted by
joshwaxman
at
10:13 AM
0
comments
![]()